发布日期:2024-05-13 14:51
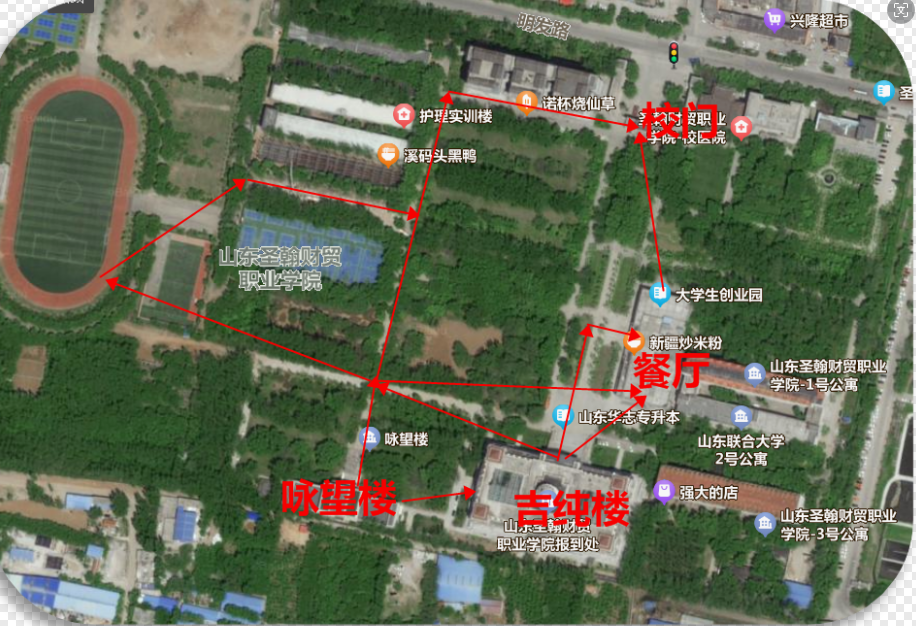
每年6、7月份,都会有很多新同学来校园参观,此时负责接待的老师就要提前设计好参观路线,而每一座建筑都有好几个出口,每一条路都能展示出校园不同的风采,那么问题来了,有没有一种可能,同学们不重复不遗漏地既可以参观到每一个建筑,又能经过校园里不同的路径回到出发点呢?
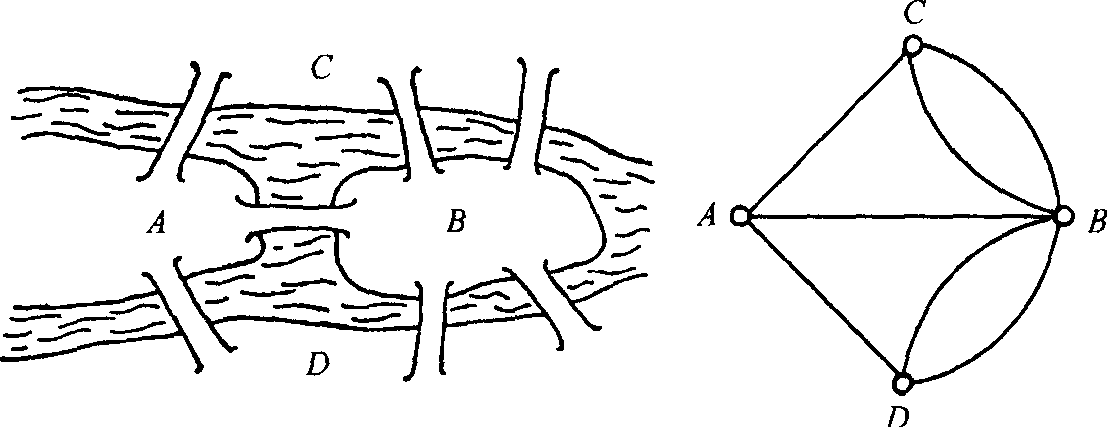
类似于上面的路线问题早已提出:在18世纪初普鲁士的哥尼斯堡城,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如下图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。
很多人对这一问题产生了兴趣,纷纷进行试验,但都未能成功,直到1736年,欧拉完美的解决了这一问题,他在交给彼得堡科学院的《哥尼斯堡七座桥》的论文报告中,阐述了他的解题方法,欧拉把它转化成一个几何问题,即一笔画问题。在解答问题的同时,开创了数学的一个新的分支——图论与几何拓扑,也由此展开了数学史上的新历程。欧拉也被称为“图论之父”。